Intercambio de claves con Diffie Hellman en Java
Hoy veremos como se hace el intercambio de claves publicas y privadas con Diffie Hellman. Primero veremos como funciona a nivel de teoría, luego veremos el código en Java.
Primero veamos como funciona la metodología del intercambio de contraseñas con Diffie Hellamn.
¿Como funciona Diffie Hellman?
En el espíritu continuo de intentar explicar los principios criptográficos mientras evito las matemáticas, voy a reutilizar un diagrama muy bueno en Wikipedia que proporciona una explicación intuitiva del proceso.
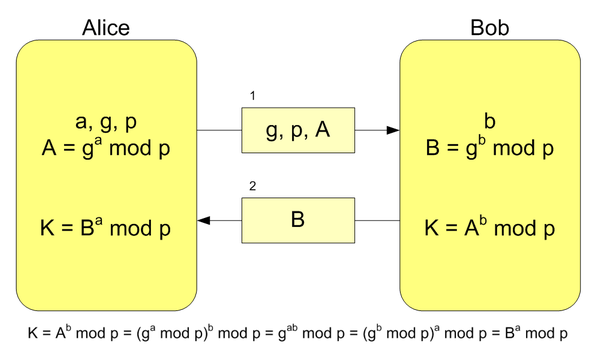
Supongamos que nuestros viejos amigos, Alice y Bob, quieren intercambiar mensajes y desean definir una clave secreta que compartirán para cifrar y descifrar mensajes.
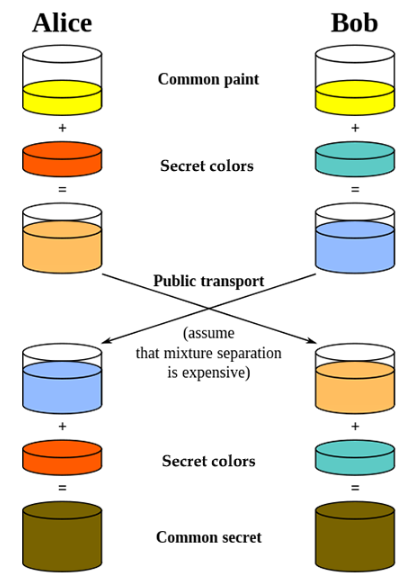
Para entender el proceso de negociación de clave DH, la analogía usa pintura de color. Las 'pinturas' en realidad son números muy largos y los procesos de mezcla son algoritmos matemáticos complejos.
Suponemos que cualquier comunicación entre Alice y Bob es fácilmente interceptable por un tercero, en este caso, la infame Eve, a quien conocimos la última vez tratando de robar documentos secretos.
- Alice y Bob eligen un color de pintura inicial
Alice y Bob comienzan seleccionando aleatoriamente un color de pintura común de una enorme biblioteca de pinturas. Aunque el diagrama a continuación muestra colores relativamente simples para mayor claridad, imagina que Alice y Bob pueden elegir entre una amplia gama de tintes, así como puedes ir a un taller de pintura donde tienen máquinas que agregan un chorro de varios tintes primarios a la pintura blanca para hacerle casi cualquier color que desee.
- Comparten este color entre sí públicamente
Supongamos que Alicia toma la iniciativa de elegir un color y le comunica su elección a Bob.
- Cada parte elige un segundo color secreto (diferente)
Cada uno de ellos ahora elige un segundo color secreto. Este color tiene una relación con el color público. El color secreto que elija Alice será diferente del color secreto que elija Bob, ya que cada uno elegirá al azar entre una enorme lista de opciones de color secretas. Esas opciones estaban determinadas por el color de pintura que originalmente eligieron para intercambiar al principio.
- Cada uno mezcla sus colores públicos y secretos y comparte sus mezclas entre sí
Ambas partes ahora mezclan sus colores secretos con sus colores públicos.
Luego intercambian el resultado entre ellos públicamente. Debido a que Alice y Bob eligieron diferentes colores secretos, las mezclas públicas que intercambian entre ellos son diferentes.
- Cada uno mezcla sus colores secretos con el color mezclado compartido de la otra parte.
Luego, Alice combina el color secreto que eligió con el color de mezcla pública que recibe de Bob.
Bob combina el color secreto que eligió con el color mezclado público que recibe de Alice
Tanto Alice como Bob ahora tienen el mismo color. Esta es la clave secreta que usarán para intercambiar mensajes.
Ahora supongamos que un atacante intercepta tanto el intercambio público original del color de pintura inicial como las mezclas de Alice y Bob. Debido a que no conocen los colores secretos que eligieron Alice y Bob, es muy difícil para ellos determinarlos a partir de la pintura mezclada.
Si pensaste que elegir el color adecuado para tu baño era un desafío suficiente, entonces puedes ver que un adversario que intercepta las elecciones de pintura pública de Alice y Bob tendría un enorme desafío tratando de reproducir su mezcla de pintura secreta.
Para realmente marcar esta casa, imagina que te di una lata de pintura rosa y te pedí que separaras cada molécula de pintura roja que se había mezclado en la lata original de pintura blanca y dime EXACTAMENTE cuántas moléculas de pintura roja tenían sido agregado. ¡Estoy seguro de que puedes ver que estoy creando un gran desafío allí! Ahora, en la analogía aquí, Alice y Bob pueden mezclar todo tipo de colores para crear su pintura común original y sus colores secretos, de modo que las mezclas que intercambian públicamente sean una mezcla de muchos colores. Como atacante, debo literalmente separar cada color, molécula por molécula. Si obtengo el resultado equivocado por una sola molécula, no pude adivinar la clave secreta.
Debido a que el uso de pintura es solo una analogía, tendrás que confiar en mí que, en comparación con ese desafío hercúleo, la ingeniería inversa de la clave secreta de los números intercambiados es aún más difícil.
Con nuestro color secreto en común, o mejor dicho, la clave secreta común, tanto Alice como Bob se podrán enviar mensajes secretos.
Código en Java
El siguiente codigo en Java consta de dos clases, Main y Person.
La clase Main contiene los llamados a la clase Person, la cual contiene los métodos necesarios para generar las claves publicas y privadas, ademas de hacer el intercambio de claves publicas, para posteriormente crear la clave privada común.
Clase Person
Contiene toda la lógica y métodos necesarios para generar e intercambiar las claves.
import javax.crypto.Cipher;
import javax.crypto.KeyAgreement;
import javax.crypto.spec.SecretKeySpec;
import java.security.KeyPair;
import java.security.KeyPairGenerator;
import java.security.PrivateKey;
import java.security.PublicKey;
public class Person {
private PrivateKey privateKey;
private PublicKey publicKey;
private PublicKey receivedPublicKey;
private byte[] secretKey;
private String secretMessage;
public void encryptAndSendMessage(final String message, final Person person) {
try {
// You can use Blowfish or another symmetric algorithm but you must adjust the key size.
final SecretKeySpec keySpec = new SecretKeySpec(secretKey, "DES");
final Cipher cipher = Cipher.getInstance("DES/ECB/PKCS5Padding");
cipher.init(Cipher.ENCRYPT_MODE, keySpec);
final byte[] encryptedMessage = cipher.doFinal(message.getBytes());
person.receiveAndDecryptMessage(encryptedMessage);
} catch (Exception e) {
e.printStackTrace();
}
}
public void generateCommonSecretKey() {
try {
final KeyAgreement keyAgreement = KeyAgreement.getInstance("DH");
keyAgreement.init(privateKey);
keyAgreement.doPhase(receivedPublicKey, true);
secretKey = shortenSecretKey(keyAgreement.generateSecret());
} catch (Exception e) {
e.printStackTrace();
}
}
public void generateKeys() {
try {
final KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("DH");
keyPairGenerator.initialize(1024);
final KeyPair keyPair = keyPairGenerator.generateKeyPair();
privateKey = keyPair.getPrivate();
publicKey = keyPair.getPublic();
} catch (Exception e) {
e.printStackTrace();
}
}
public PublicKey getPublicKey() {
return publicKey;
}
public void receiveAndDecryptMessage(final byte[] message) {
try {
// You can use Blowfish or another symmetric algorithm but you must adjust the key size.
final SecretKeySpec keySpec = new SecretKeySpec(secretKey, "DES");
final Cipher cipher = Cipher.getInstance("DES/ECB/PKCS5Padding");
cipher.init(Cipher.DECRYPT_MODE, keySpec);
secretMessage = new String(cipher.doFinal(message));
} catch (Exception e) {
e.printStackTrace();
}
}
/**
* In a real life example you must serialize the public key for transferring.
*
* @param person
*/
public void receivePublicKeyFrom(final Person person) {
receivedPublicKey = person.getPublicKey();
}
//~ ----------------------------------------------------------------------------------------------------------------
public void whisperTheSecretMessage() {
System.out.println(secretMessage);
}
/**
* 1024 bit symmetric key size is so big for DES so we must shorten the key size. You can get first 8 longKey of the
* byte array or can use a key factory
*
* @param longKey
*
* @return
*/
private byte[] shortenSecretKey(final byte[] longKey) {
try {
// Use 8 bytes (64 bits) for DES, 6 bytes (48 bits) for Blowfish
final byte[] shortenedKey = new byte[8];
System.arraycopy(longKey, 0, shortenedKey, 0, shortenedKey.length);
return shortenedKey;
// Below lines can be more secure
// final SecretKeyFactory keyFactory = SecretKeyFactory.getInstance("DES");
// final DESKeySpec desSpec = new DESKeySpec(longKey);
//
// return keyFactory.generateSecret(desSpec).getEncoded();
} catch (Exception e) {
e.printStackTrace();
}
return null;
}
}
Clase Main
Se hacen los llamados. Es importante entender en que orden se deben hacer los llamados a los diferentes métodos, pues de lo contrario no funcionara.
public class Main {
//~ --- [METHODS] --------------------------------------------------------------------------------------------------
public static void main(final String[] args) throws Exception {
new Main().init();
}
//~ --- [METHODS] --------------------------------------------------------------------------------------------------
private void init() {
// 1. ------------------------------------------------------------------
// This is Alice and Bob
// Alice and Bob want to chat securely. But how?
final Person alice = new Person();
final Person bob = new Person();
// ? ?
//
// O O
// /|\ /|\
// / \ / \
//
// ALICE BOB
// 2. ------------------------------------------------------------------
// Alice and Bob generate public and private keys.
alice.generateKeys();
bob.generateKeys();
//
// O O
// /|\ /|\
// / \ / \
//
// ALICE BOB
// _ PUBLIC KEY _ PUBLIC KEY
// _ PRIVATE KEY _ PRIVATE KEY
// 3. ------------------------------------------------------------------
// Alice and Bob exchange public keys with each other.
alice.receivePublicKeyFrom(bob);
bob.receivePublicKeyFrom(alice);
//
// O O
// /|\ /|\
// / \ / \
//
// ALICE BOB
// + public key + public key
// + private key + private key
// _ PUBLIC KEY <-------------------------> _ PUBLIC KEY
// 4. ------------------------------------------------------------------
// Alice generates common secret key via using her private key and Bob's public key.
// Bob generates common secret key via using his private key and Alice's public key.
// Both secret keys are equal without TRANSFERRING. This is the magic of Diffie-Helman algorithm.
alice.generateCommonSecretKey();
bob.generateCommonSecretKey();
//
// O O
// /|\ /|\
// / \ / \
//
// ALICE BOB
// + public key + public key
// + private key + private key
// + public key + public key
// _ SECRET KEY _ SECRET KEY
// 5. ------------------------------------------------------------------
// Alice encrypts message using the secret key and sends to Bob
alice.encryptAndSendMessage("Bob! Guess Who I am.", bob);
//
// O O
// /|\ []--------------------------------> /|\
// / \ / \
//
// ALICE BOB
// + public key + public key
// + private key + private key
// + public key + public key
// + secret key + secret key
// + message _ MESSAGE
// 6. ------------------------------------------------------------------
// Bob receives the important message and decrypts with secret key.
bob.whisperTheSecretMessage();
//
// O ((( ((( ((( \O/ )))
// /|\ |
// / \ / \
//
// ALICE BOB
// + public key + public key
// + private key + private key
// + public key + public key
// + secret key + secret key
// + message + message
}
}
Espero que este articulo te haya ayudado en tus dudas.
Si quieres conocer otros artículos parecidos a Intercambio de claves con Diffie Hellman en Java puedes visitar la categoría Java.
Entradas relacionadas